고정 헤더 영역
상세 컨텐츠
본문

Writer: Harim Kang
해당 포스팅은 '시작하세요! 텐서플로 2.0 프로그래밍'책의 흐름을 따라가면서, 책 이외에 검색 및 다양한 자료들을 통해 공부하면서 정리한 내용의 포스팅입니다. 해당 내용은 AND, OR, XOR 신경망 만드는 법에 대한 내용을 담고 있습니다.
2020/02/06 - [IT/Deep Learning] - 딥러닝 (2) - 텐서플로우 2.0 기초와 뉴런 만들기
딥러닝 (2) - 텐서플로우 2.0 기초와 뉴런 만들기
Writer: Harim Kang 해당 포스팅은 '시작하세요! 텐서플로 2.0 프로그래밍'책의 흐름을 따라가면서, 책 이외에 검색 및 다양한 자료들을 통해 공부하면서 정리한 내용의 포스팅입니다. 해당 내용은 텐서플로우 2...
davinci-ai.tistory.com
위의 포스팅에 이어지는 내용입니다.
간단한 신경망 네트워크 만들기
실습 예제
이번 포스팅에서도 지난번 사용했던, sigmoid를 사용하겠습니다.
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))AND 연산 네트워크
AND연산은 프로그래밍 언어를 배울 때 한번 씩은 들어본 연산이라고 생각합니다. 아래와 같은 연산을 뜻합니다. 항상 참일 때만, 참을 결과로 출력하는 연산입니다.

이것을 numpy 배열로 나타내면 아래와 같이 선언합니다.
x = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([[1], [0], [0], [0]])또한 가중치와 편향도 정규 분포를 가지는 난수로 초기화 해줍니다. 또한, 학습률은 0.1로 설정하였습니다. 이때 아래의 공식과 같이 input값이 두개이므로, 가중치도 각각에 맞춰서 두개를 선언해줍니다.

import tensorflow as tf
w = tf.random.normal([2], 0, 1)
b = tf.random.normal([1], 0, 1)
a = 0.1이제 학습을 시켜보겠습니다. 이전 포스팅에서 만든 편향을 가진 뉴런처럼 코드를 구성하면 됩니다. 각각 네가지 경우를 한번씩 학습할 때마다, 네가지 를 예측한 값과 실제 값의 차이인 error값의 합을 구해서 살펴보겠습니다.
for i in range(10000):
error_sum = 0
for j in range(4):
output = sigmoid(np.sum(x[j]*w)+b)
error = y[j][0] - output
w = w + x[j] * a * error
b = b + a * error
error_sum += error
if i % 1000 == 999:
print(i, error_sum)저는 10000번을 반복 학습하였습니다. 1000번에 한번씩 error값을 확인하였습니다.

위와 같이, 학습을 진행할수록 0에 가까운 error값을 확인할 수 있습니다.
이제 학습시켜서 나온 가중치와 편향을 사용하여 각각의 케이스를 예측해 보겠습니다.
for i in range(4):
print('X:', x[i], 'Y:', y[i], 'Output:', sigmoid(np.sum(x[i]*w)+b))
위와 같이, 실제로 1이 나와야하는 값은 1에 가깝게, 0에 가까워야하는 값은 0에 가깝게 예측이 되었습니다. [0 0] 케이스의 경우에는 다른 케이스들 보다 더 0에 가까운걸로 보아 더 확실한 케이스라는 점을 알 수 있습니다.
OR 연산 네트워크
OR연산 또한 AND연산과 비슷합니다. 다른 점은, 하나라도 참이라면 결과가 참이라는 점입니다.
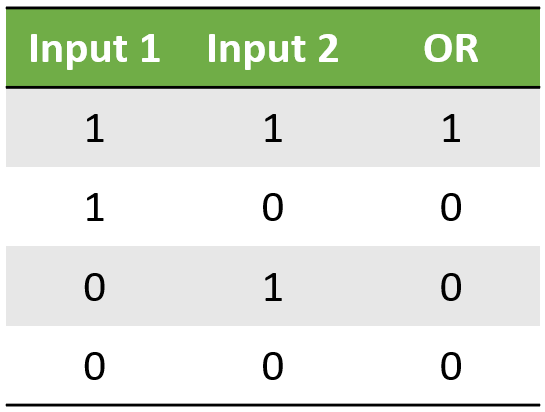
위의 케이스들도 numpy 배열로 바꾸어보겠습니다.
x = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([[1], [1], [1], [0]])이외의 가중치와 편향과 학습률 및 학습 코드는 AND연산과 똑같습니다. 이제 학습을 시키면 결과는 아래와 같습니다.
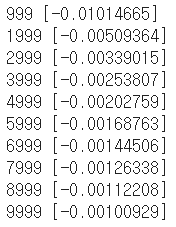
학습을 진행할 수록 error값의 합이 0에 가까워지는것을 확인할 수 있습니다. 각각의 케이스들을 해당 가중치와 편향으로 예측해보겠습니다.

[1 1] 케이스의 경우에는 확실하게 1이라고 단정지은 것 같습니다. 그리고 [0 0] 케이스는 0에 가깝고 나머지 케이스들은 1에 가까운걸로 보아 잘 학습이 된거 같습니다.
XOR 연산 네트워크
XOR은 AND나 OR연산과는 다르게 홀수 개의 입력이 참일 때, 결과가 참이 됩니다. 입력을 두개로 제한한다면, 아래의 표와 같습니다.

AND와 OR연산 때와 같이, y 배열 부분의 케이스만 바꾸어서 코드를 똑같이 돌려보겠습니다.
10000번을 시도하니 에러 값이 모두 0이 나와서 2000번으로 줄여서 학습을 진행하였습니다.

위와 같이, 특정 학습 지점부터 에러 값이 0이 나와 버리고 있습니다. 이것이 과연 학습이 잘된걸까요? 계산된 가중치와 편향을 가지고 각 케이스를 계산해보았습니다.

위와 같이, 결과가 0이 나와야하든지, 1이 나와야하든지, 모든 케이스가 0.5에 가깝게 나오고 있습니다. 이것은 원하던 결과가 아닙니다.
단층 퍼셉트론에서의 XOR 문제점
결과를 해석해보자면, 가중치와 편향 값은 모두 케이스 순서에 의존적이 된다는 것을 알 수 있습니다. 먼저 들어간 [1 1]이라는 케이스가 네번째에 들어가는 [0 0]이라는 케이스보다 영향을 준다는 것입니다. [1 1]이라는 케이스가 먼저 들어가서 가중치와 편향에 중대한 영향을 미치고 이 값들을 가지고 학습을 진행한다는 것이 문제입니다.

위와 같은 이유로 가중치를 살펴보니, 첫번째와 두번째 가중치 모두 0에 가깝게 비슷한 수치를 나타내고 있습니다. 중요도가 어떤 것이 더 높은지 알지못한다는 의미입니다. 편향 또한 영향이 미비해질 만큼 작은 수치를 나타내고 있습니다. 이러한 이유들로 인하여 XOR문제가 생깁니다.
인공 신경망에서는 단층 퍼셉트론으로 XOR 연산이 불가능하다는 것은 마빈 민스키 등에 의해서 밝혀졌습니다. 이러한 내용이 밝혀지면서 인공지능의 겨울이 찾아왔었습니다.
그러면 XOR문제는 풀지 못하는 걸까요? 여러 층의 퍼셉트론을 사용하면 해결이 됩니다.
다층 XOR 연산 신경망
다층 구조의 신경망을 설계해보겠습니다.

2단의 Dense Layer로 구성하였습니다. Dense는 기본적인 레이어로, 입력과 출력 사이에 있는 모든 뉴런이 서로 연결되어 있는 레이어입니다. Dense Layer는 아래와 같이 선언이 가능합니다.
tf.keras.layers.Dense()각각의 Layer는 순차적으로 배치되어있습니다. 이를 Sequential 신경망이라고 합니다. 이것은 아래와 같이 선언합니다.
tf.keras.Sequential()Sequential한 Dense Layer를 2층으로 쌓아보겠습니다.
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=2, activation='sigmoid', input_shape=(2,)),
tf.keras.layers.Dense(units=1, activation='sigmoid')
])순차적인 신경망안에 두개의 Dense Layer를 배치하고, 첫번째 Dense Layer는 2개의 뉴런을 선언하였고, 각 뉴런은 sigmoid를 활성함수로 가집니다. 입력 값은 두개이므로 모양이 (2,) 모양입니다. 두번째 Dense Layer는 1개의 뉴런을 선언하고, 마찬가지로 sigmoid 활성함수를 사용하였습니다.
XOR연산이므로, x와 y값은 그대로 입니다.
x = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([[0], [1], [1], [0]])이제는 model을 준비시키는 명령어를 사용하여 최적화 함수(optimizer)와 손실 함수(loss)를 정의하겠습니다.
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), loss='mse')tf.keras에서는 다양한 최적화 함수와 손실 함수를 제공합니다.

그 중에서도 SGD(Stochastic Gradient Descent)는 확률적 경사 하강법이라고 합니다. 경사 하강법은 앞선 포스팅에서 설명하였고, 이 경사 하강법을 한번에 계산(전체 데이터세트를 사용)하지 않고 확률을 이용하여 부분적으로 나눠서 계산을 한다는 의미입니다.
- SGD(Stochastic Gradient Descent)
- 기존의 경사 하강법은 데이터세트의 크기가 너무 커지면 계산이 오래 걸리는 단점이 있었습니다.
- SGD는 반복당 하나의 데이터(Batch=1)만을 사용하여 적은 계산으로 기울기를 얻어내는 방식입니다.
- 단점: 반복이 충분하면 효과는 좋지만, 노이즈가 심합니다. 최저점을 찾는다는 보장이 없습니다. 가능성만 높을 뿐입니다.
- 위의 단점을 극복하기 위해서 미니 배치 SGD가 있습니다. 배치를 너무 크게도 너무 작게도 잡지 않고 SGD보다 노이즈는 적게, 일반 경사 하강법보다는 효율적으로 찾는 방식입니다.
손실 함수(Loss Function)은 앞선 포스팅(https://davinci-ai.tistory.com/14?category=876949)에서 설명된 RMSE의 제곱인 MSE를 사용하였습니다.
model.summary()위의 코드를 사용하여 형성된 신경망의 구조를 살펴볼 수 있습니다.

파라미터는 첫번째 Layer에서 입력값들이 뉴런에 전달되는 2*2개인 4개에 편향이 각 뉴런에 전달되어 총 6개입니다. 두번째 Layer에서는 첫 Layer에서 나온 출력 값 두개와 편향을 합쳐서 총 3개의 값이 두번째 층에 전달되어 결과적으로 하나의 출력 값이 나오게 됩니다.
history = model.fit(x, y, epochs=2000, batch_size=1)위는 모델을 학습 시키는 코드입니다. x와 y변수들을 전달하여 학습데이터로 사용하고, 2000번 반복한다는 의미입니다.

학습을 진행하면 위와 같은 출력이 나오며, 손실 값을 알려줍니다. 학습을 진행할수록 0에 가까워지는 것을 확인할 수 있습니다.
이제 제대로 학습이 되었는지 확인해보겠습니다.
model.predict(x)위의 코드를 통해서 x에 대한 예측 값을 출력 받을 수 있습니다.

정답은 0, 1, 1, 0 순서입니다. 각각 0과 1에 해당하는 수에 가깝게 나오고 있는것을 확인 할 수 있습니다. 이는 학습을 더 많이 할수록 더 정답에 해당하는 수치로 갈것 입니다.
이제는 가중치와 편향 값을 확인해보겠습니다.
for weight in model.weights:
print(weight)
위와 같은 출력을 얻을 수 있고, 이를 그림에 표현해보면 아래와 같습니다.

단층의 연산 신경망에 비해 가중치와 편향 값이 0에 가깝지 않고 뚜렷한 것을 확인할 수 있습니다.
(참고!) 인간의 뇌는 XOR 연산이 한층으로도 가능하다?
XOR 단층 퍼셉트론 문제는 인공 신경망에서는 불가능하다는 결론이 있습니다. 물론 non-linear 문제의 경우에는 학습이 되는 경우가 생기기도 하지만, 확실하게 가능한 예제는 못보았습니다. 인간의 뉴런은 어떨까요?
https://science.sciencemag.org/content/367/6473/83?fbclid=IwAR0T6N-YbkK-LuEaFbu2Gq9uRXzsJwqZF-rqAYB63eREsxXiT5iADHmgmLI
위의 연구내용은 인간의 뉴런이 한층으로도 XOR연산이 가능하다는 것을 밝혀낸 연구입니다. 인간의 뇌는 발달 단계에서 대뇌 피질의 2/3 층이 뷸균형적으로 두터워지는데 이 층을 구성하는 피라미드 신경세포와 수상돌기의 수가 매우 많아서 가능한 일이라고 합니다. 해당 피질 층의 피라미드 신경세포를 외과적으로 추출해서 시험해 본 결과 한개의 신경세포에서 XOR 연산이 가능하다는 결론을 내렸다고합니다.
Dendritic action potentials and computation in human layer 2/3 cortical neurons
A special developmental program in the human brain drives the disproportionate thickening of cortical layer 2/3. This suggests that the expansion of layer 2/3, along with its numerous neurons and their large dendrites, may contribute to what makes us human
science.sciencemag.org
XOR 네트워크 구성 요약
아래의 코드는 데이터 준비, 모델 선정 및 구성, 모델 학습, 모델 예측의 순서 코드입니다.
import tensorflow as tf
import numpy as np
x = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([[0], [1], [1], [0]])
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=2, activation='sigmoid', input_shape=(2,)),
tf.keras.layers.Dense(units=1, activation='sigmoid')
])
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), loss='mse')
history = model.fit(x, y, epochs=2000, batch_size=1)
model.predict(x)실습 코드는 https://github.com/harimkang/tensorflow2_deeplearning/blob/master/tensor2_2.ipynb에서 확인하실 수 있습니다.
https://github.com/harimkang/tensorflow2_deeplearning/blob/master/tensor2_2.ipynb
harimkang/tensorflow2_deeplearning
tensorflow2, deep learning study example codes. Contribute to harimkang/tensorflow2_deeplearning development by creating an account on GitHub.
github.com
Reference
'IT > Deep Learning' 카테고리의 다른 글
| 딥러닝 (6) - CNN (Convolutional Neural Network) (2) | 2020.02.24 |
|---|---|
| 딥러닝 (5) - 분류(Classification) 네트워크 (1) | 2020.02.24 |
| 딥러닝 (4) - 회귀(Regression) 네트워크 만들기 (0) | 2020.02.12 |
| 딥러닝 (2) - 텐서플로우 2.0 기초와 뉴런 만들기 (2) | 2020.02.06 |
| 딥러닝 (1) - Deep Learning 소개 및 용어 정리 (0) | 2020.02.04 |




